Método de Monte Carlo
Ao longo dos séculos, os Matemáticos criaram vários métodos para calcular o valor de π.
O Método de Monte Carlo é um termo utilizado para se referir a qualquer método que resolve um problema gerando números aleatórios e observando se uma dada fração desses números satisfaz uma propriedade previamente estabelecida.
A ideia é colocar a circunferência dentro de uma figura, cuja área seja fácil de calcular, e calcular pontos aleatórios dentro da figura. Utilizaremos um quadrado de lado 1 e um quarto de circuferência.
Se o ponto sorteado estiver dentro da circunferência, então marcamos um acerto. Ao final dos sorteios, espera-se que a área da circunferência seja proporcional à taxa de acertos e à área do quadrado. Esse valor será uma aproximação para π. "Espera-se" porque o método é estocástico, isto é, os resultados obtidos são aleatórios. Porém, para uma grande amostra de pontos, ele deve convergir para o resultado esperado, ou seja, π.
Neste caso, espera-se que \(\frac{\pi}{4}\approx\frac{N_{acertos}}{N_{pontos}}\)
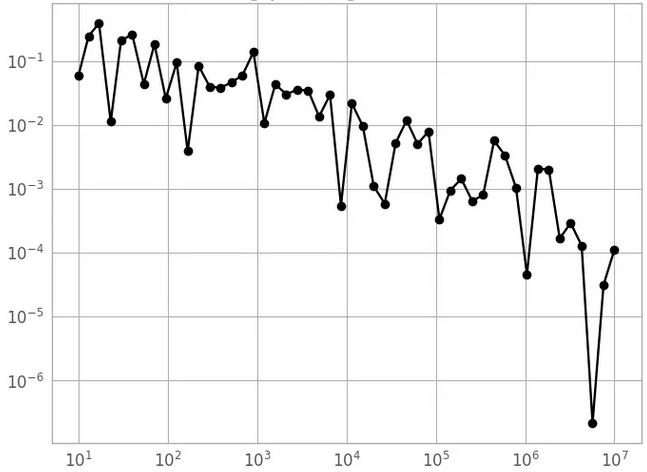
Este gráfico mostra um exemplo da relação entre o erro na estimativa de pi e o tamanho da amostra. O eixo x representa o tamanho da amostra e o eixo y representa o erro absoluto na estimativa de pi. O erro diminui à medida que o tamanho da amostra aumenta, mas ainda existe alguma aleatoriedade nas estimativas, mesmo para tamanhos de amostra grandes.
Index